Gravitation Class 10 Notes Maharashtra Board

Std 10 Science Part 1 Chapter 1 Gravitation Notes Maharashtra Board

Class 10 Science Part 1 Chapter 1 Gravitation Notes Maharashtra Board

Introduction:

Sir Issac Newton discovered the phenomenon of gravitation, when apple fell from
tree.
He thought why apple fell in vertical downward direction and not at any angle at
vertical or horizontal direction.
After thinking, he came to conclusion that earth attracts objects towards its centre.
Thus apple fell in vertical direction towards the earth.
Gravity is responsible for revolution of moon around the sun, planets around the
sun.

Simple definition of gravitation / gravity:

Gravity is the force that attracts all objects toward each other.
It keeps us on the ground and makes things fall when dropped.
Gravity also keeps the Moon in orbit around the Earth and the planets around
the Sun.

Force and Motion:

A) Circular Motion:

When an object travels in circular path i.e. it comes back to its initial point after
completing path in circular direction is called circular motion.
When objects travels with uniform speed, covers equal distance in equal intervals of
time in circular direction it is called as uniform circular motion.

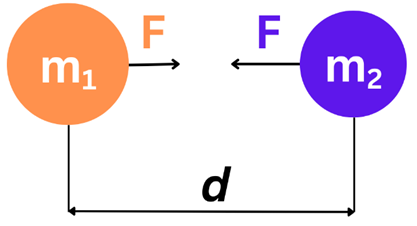
B) Centripetal Force:

A force acts on any object moving along a circle and it is directed towards the centre
of the circle. This is called the Centripetal force.
Formula of centripetal force:

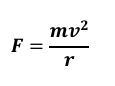
Where: F= Centripetal force
m= mass of object
v= speed of object
r= radius of circular path

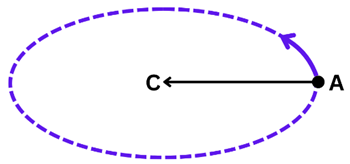
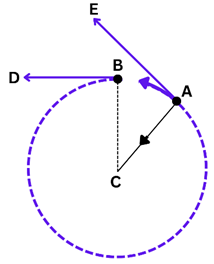
Consider diagram 2 where C is the centre of circle. Let AC be the string and Point A
be the stone tied to string.
When we start moving string in circular direction, the stone is directed towards the
centre C as long as we are holding the string.
If we release the string the centripetal force (force directing stone towards the
centre) stops and stone is released in straight line BD.
This is also called as tangential direction.
Ray AE and BD represent the tangential direction when stone is released.

Kepler’s Laws:

A) Kepler’s First Law:

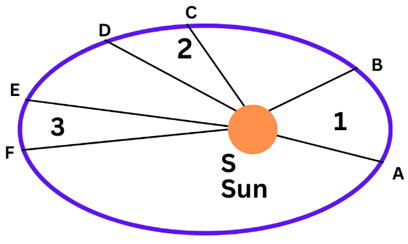
The orbit of a planet is an ellipse with the Sun at one of the foci.
Diagram 3 shows the elliptical orbit of a planet revolving around the sun. The position of the Sun is indicated by S.

B) Kepler’s Second Law:

The line joining the planet and the Sun sweeps equal areas in equal intervals of
time.
AB and CD are distances covered by the planet in equal time i.e. after equal intervals
of time.
The positions of the planet starting from A and C are shown by B and D respectively.
The straight lines AS and CS sweep equal area in equal interval of time i.e. area ASB
and CSD are equal.

C) Kepler’s Third Law:

The square of planet’s period of revolution around the Sun is directly proportional
to the cube of the mean distance of a planet from the Sun.
If r is the average distance of the planet from the Sun and T is its period of revolution
then,

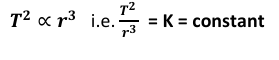
Newton’s Universal Law of Gravitation:

Where G= Universal Gravitational Constant

3. The mass of one object is doubled, the force between the two objects also doubles.
4. If the distance is doubled, the force decreases by a factor of 4.
5. Newton’s law of gravitation states that, “Every particle in the universe attracts
every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their
centres.”

Value of G (gravitational constant) and SI unit:

Value of gravitational constant:

Centre of mass:

The point inside or outside the object at which the total mass of the object is
concentrated is called as the centre of mass.
A spherical object having uniform density has centre of mass at its geometrical
centre.
The centre of mass of any object having uniform density is at its centroid.

Uniform circular motion / Magnitude of centripetal force:

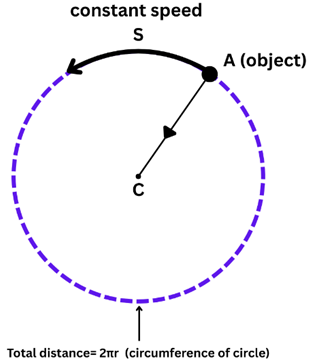
Consider a planet A is moving with constant speed S in a circular path.
Centripetal force is directing the moving planet A towards the centre C i.e. Sun.
Let m be the mass of planet, v be the velocity of planet and r be the radius of the
orbit.

4. Let the time of revolution of planet around sun be T.
The distance travelled by the planet in one revolution =perimeter of the orbit 2πr

We know that,

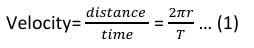
Also,

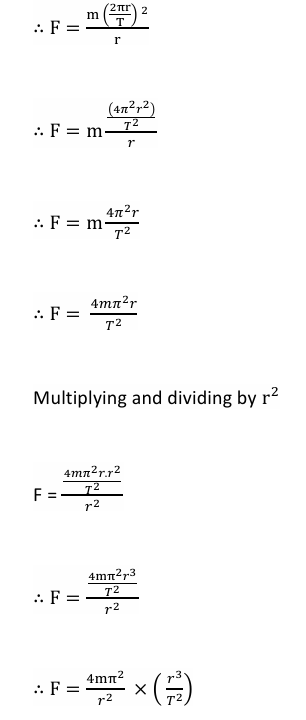
According to Kepler’s third law,

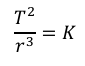
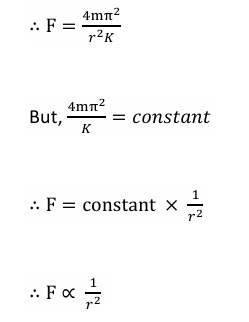
Earth’ gravitational force:

The centre of mass of the earth is situated at its centre, so the gravitational force on
any object due to the earth is always directed towards the centre of the earth.
Because of this force, an object falls vertically downwards on the earth.

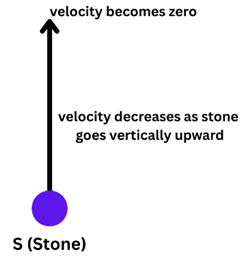
3. If a stone is thrown vertically upward, gravitational force of earth pulls stone
towards itself.
4. Because of this downward pull, velocity of the stone decreases and at a point
upwards, its velocity becomes zero.
5. At this point stone starts falling to the ground in vertically downward direction.

Earth’s gravitational acceleration:

According to Newton’s second law of motion, a force acting on a body results in its
acceleration.
Thus, the gravitational force due to the earth on a body results in its acceleration.
This is called acceleration due to gravity and is denoted by ‘g’.
The direction of the acceleration due to gravity is directed towards the centre of the
earth i.e. vertically downwards.

Value of g on the surface of earth:

According to Newton’s law of gravitation,

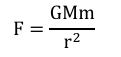
But, F= mg … (g is acceleration due to gravity)

Variation in value of g:

A) Change along the surface of the earth :

The shape of earth is not exactly spherical.
From place to place the distance of point on the surface of the earth from its centre
differs.
Due to its rotation, the earth bulges at the equator and is flatter at the poles.
Its radius is largest at the equator and smallest at the poles.

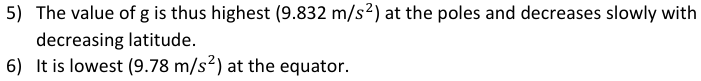
B) Change with height :

As we go above the earth’s surface, the value of r increases and the value of g
decreases.
However, the decrease is rather small for heights which are small in comparison to
the earth’s radius.

C) Change with depth:

The value of g changes as we go inside the earth. The value of r decreases.
However, the part of the earth which contributes towards the gravitation al force
felt by the object also decreases.
The value of M also decreases.
As a combined result of change in r and M, the value of g decreases as we go deep
inside the earth.

Mass and Weight:

A) Mass:

Mass is the amount of matter present in the object.
The SI unit of mass is kg.
Mass is a scalar quantity.
Its value is same everywhere.
Its value does not change even when we go to another planet.
According to Newton’s first law, mass is the measure of the inertia of an object.
Higher the mass, higher is the inertia.

B) Weight:

1. The weight of an object is defined as the force with which the earth attracts the
object.
2. The force (F) on an object of mass m on the surface of the earth is,
W𝐞𝐢𝐠𝐡𝐭 (𝐖) = 𝐅 =𝐦𝐠
where,

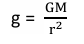
3. SI unit of weight is Newton.
4. The weight is a vector quantity and its direction is towards the centre of the earth.
5. As the value of g is not same everywhere, the weight of an object changes from
place to place, though its mass is constant everywhere.

Free fall:

Whenever an object moves under the influence of the force of gravity alone, it is said
to be falling freely.
Any object falling towards the earth is in free fall.
In free fall, the initial velocity of the object is zero and goes on increasing due to the
acceleration due to gravity of the earth.
During free fall, the frictional force due to air opposes the motion of the object and a
buoyant force also acts on the object. Thus, true free fall is possible only in vacuum.
For a freely falling object, the velocity on reaching the earth and the time taken for it
can be calculated by using Newton’s equations of motion. For free fall, the initial
velocity u = 0 and the acceleration a = g. Thus we can write the equations as:

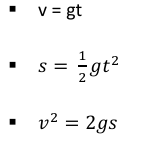
6. For calculating the motion of an object thrown upwards, acceleration is negative, i.e.
in a direction opposite to the velocity and is taken to be – g.
7. The magnitude of g is the same but the velocity of the object decreases because of
this negative acceleration.

Gravitational Potential Energy:

1. The energy stored in an object because of its position or state is called potential
energy.
2. This energy is relative and increases as we go to greater heights from the surface of
the earth.
3. The potential energy of an object of mass m, at a height h from the ground is mgh
and on the ground is zero.
4. When h is small compared to the radius R of the earth, we can assume g to be
constant and can use the formula (mgh).
5. But for large values of h, the value of g decreases with increase in h.
6. For an object at infinite distance from the earth, the value of g is zero and earth’s
gravitational force does not act on the object.
7. So it is more appropriate to assume the value of potential energy to be zero there.
8. Thus, for smaller distances, i.e. heights, the potential energy is less than zero, i.e. it is
negative.

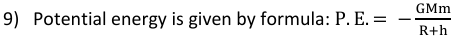
Where, h = height from the surface of the earth
M and R are earth’s mass and radius respectively

Escape velocity:

Escape velocity is the minimum speed an object must have to break free from the
gravitational pull of planet or any object.
Let,
M = Mass of the planet
m = Mass of the object
r = distance from the centre of the planet to the object
G = gravitational constant
v = escape velocity

A) Total Energy at the Surface:

Kinetic Energy:

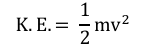
Gravitational potential energy:

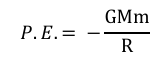
(Negative because gravity is an attractive force)

B) Total Energy at Infinity:

At infinite distance from the planet:
1. Kinetic energy = 0
2. Gravitational potential energy = 0
3. So total energy = 0

Now, Total energy at surface=Total energy at infinity

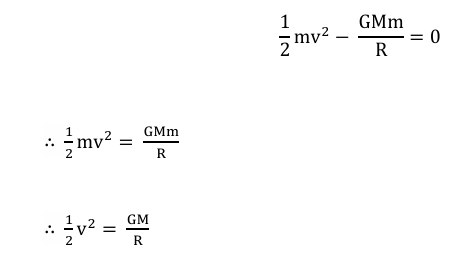
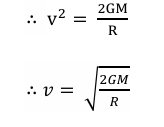
This is the expression for escape velocity
We know that,

Therefore, escape velocity of earth is:

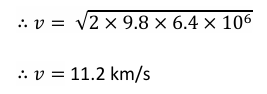
Solutions for the exercises, unsolved numerical problems, and solved examples will soon be available for download in convenient PDF format at very affordable prices. Our notes are carefully crafted, accurate, and aligned with board requirements to help you succeed.